answer:: 1. Given the ellipse in standard form is: [ frac{x^2}{a^2} + frac{y^2}{b^2} = 1 quad text{with} quad a > b > 0 ] The foci of the ellipse are at points ( F_1(-c, 0) ) and ( F_2(c, 0) ) where ( c^2 = a^2 - b^2 ). 2. Let ( Q ) be a point on the ellipse not at the vertices ( (pm a, 0) ). An exterior bisector of ( angle F_1 Q F_2 ) is drawn passing through ( F_1 ) or ( F_2 ), which intersects the ellipse at ( Q ) and bisects at point ( P ). 3. Extend ( F_1P ) to meet the extension of ( F_2Q ) at point ( R ). 4. Because ( Q ) lies on the ellipse, we use the property that the sum of distances from any point on the ellipse to the foci is constant and equals ( 2a ). Thus: [ |Q F_1| + |Q F_2| = 2a ] 5. The point ( R ) is such that: [ |R F_2| = |Q R| + |Q F_2| ] Using the property of the ellipse, we equate: [ |Q F_1| + |Q F_2| = 2a implies |R F_2| = 2a ] 6. The perpendicular distance ( |O P| ) from the origin (center of the ellipse) to ( P ) is given by half the distance ( |R F_2| ): [ |O P| = frac{1}{2} |R F_2| = a ] This confirms the point ( P ) we are looking at is at a distance ( a ) from the center. 7. Therefore, the point ( P )'s locus, excluding ( (-a, 0) ) and ( (a, 0) ) due to the exclusion of the vertices, forms a circle with radius ( a ) centered at the origin. **Conclusion**: The locus of point ( P ) is a circle with center at the origin and radius ( a ), excluding the points ( (-a, 0) ) and ( (a, 0) ). [ boxed{text{A circle centered at the origin with radius } a text{, excluding } (-a, 0) text{ and } (a, 0).} ]

answer:Let's consider the problem where we want to determine the maximum number of triangles into which a triangle ( T ) can be subdivided, such that the same number of segments meet at each node, and none of these segments should break the sides of the original triangle ( T ). 1. Suppose we have a subdivision of the triangle ( T ) that satisfies the conditions of the problem. Let ( k ) be the number of segments converging at any node. Let ( A ) be one such node in our subdivided network: 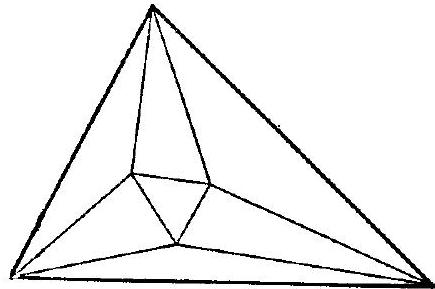 **Fig. 58**: Example where ( k = 4 ). 2. Let ( A ) be one of the nodes in our network. The sum of all angles at node ( A ) for the regions adjoining ( A ) (including the "external" area ( T_1 ), or "ocean" surrounding the "island" ( T ), divided into certain number ( C ) of triangular "countries") equals ( 360^circ ). Thus, the total sum of angles of all regions (triangles) and the external area ( T_1 ) is ( 360^circ Y ), where ( Y ) denotes the total number of nodes (including the three vertices of triangle ( T )). On the other hand, the total sum of angles for ( C ) triangles and the area ( T_1 ) is: [ 180^circ times C + left(3 times 360^circ - 180^circright) = 180^circ times C + 900^circ ] Here, the last term ( 900^circ ) expresses the sum of angles of the area ( T_1 ). Therefore, we have: [ 360^circ cdot Y = 180^circ cdot C + 900^circ ] Simplifying, we get: [ 2Y = C + 5 ] 3. Given that each node has ( k ) segments radiating out from it (where ( T_1 ), the "ocean," is also considered a "country"), the sum of segments originating from each of ( Y ) nodes gives ( k Y ), which obviously equals double the number ( Gamma ) of boundaries, as each boundary is counted twice per the two nodes it connects: [ k Y = 2 Gamma ] And since every one of ( C + 1 ) "countries" (including the ocean ( T_1 )) has exactly 3 boundaries, where each boundary separates two "countries": [ 3(C + 1) = 2 Gamma, quad text{so} quad Gamma = frac{3}{2}(C + 1) ] 4. Substituting the value of ( Gamma ) and ( Y ), we get: [ k Y = 2 Gamma implies Y = frac{2 Gamma}{k} = frac{3}{k}(C + 1) ] From the previous expressions, we also have: [ 3(C + 1) = 2 Gamma implies Gamma = frac{3}{2} C + frac{3}{2} ] Therefore, [ 2Y = C + 5 implies Y = frac{1}{k} left(2 Gammaright) = frac{3}{k} C + frac{3}{k} ] 5. By substituting these into the main relation ( C = frac{k}{3} Y - 1 ), [ C = frac{k}{3} Y - 1 = frac{k}{3} left(frac{3}{k} C + frac{3}{k}right) - 1 = C + 1 ] Simplifying, we obtain: [ (6 - k) C = 5k - 6 ] Hence, [ C = frac{5k - 6}{6 - k} ] 6. The expression for ( C ) is positive only when ( k = 2, 3, 4 ) and ( 5 ), yielding ( C = 1, 3, 7 ) and 19. All these values, based on the problem's requirements (as seen in figures), are possible. The highest value is: [ C = 19 ] **Conclusion**: Therefore, the triangle ( T ) can be subdivided into at most 19 triangles under the given conditions. [ boxed{19} ]

answer:The waiter started with 29 customers and added another 20 during the lunch rush, so the total number of customers he waited on is 29 + 20 = 49 customers. If 15 customers left a tip, then the number of customers who didn't leave a tip is the total number of customers minus the number who did leave a tip. So, the number of customers who didn't leave a tip is 49 - 15 = boxed{34} customers.

answer:Given that a= sqrt {3}, b=1, and angle B=30^{circ}, we can apply the sine law (law of sines) to find angle A. The sine law states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides of the triangle. So, we have: frac{a}{sin A} = frac{b}{sin B} Substituting the given values, we get: frac{sqrt {3}}{sin A} = frac{1}{sin 30^{circ}} Solving for sin A, we obtain: sin A = sqrt {3} cdot sin 30^{circ} = sqrt {3} cdot frac{1}{2} = frac{sqrt {3}}{2} Since angle A is an angle within a triangle, it must be between 0 and pi radians (or 0 and 180 degrees). Thus, there are two possible values for angle A: angle A = sin^{-1} left(frac{sqrt {3}}{2}right) = frac{pi}{3} text{ radians (or } 60^{circ}) or angle A = pi - sin^{-1} left(frac{sqrt {3}}{2}right) = frac{2pi}{3} text{ radians (or } 120^{circ}) However, given that angle B = 30^{circ}, the only valid solution for angle A that results in a triangle with valid angle measures is: angle A = boxed{frac{pi}{3} text{ radians (or } 60^{circ})}